TJCTF MISC部分
01 guess-my-number
可以直接kali连接去自己猜一猜，也可以自己写个脚本让他自己猜。
from pwn import *
def auto_guess():
# 连接远程服务器
conn = remote('tjc.tf', 31700)
low = 1
high = 1000
for _ in range(10):
guess = (low + high) // 2
conn.recvuntil(b"Guess a number from 1 to 1000:")
conn.sendline(str(guess).encode())
res = conn.recvline().decode()
print(f"Guessed {guess} -> {res.strip()}")
if "Too low" in res:
low = guess + 1
elif "Too high" in res:
high = guess - 1
elif "You won" in res:
# 打印剩余信息（包含 flag）
print(conn.recvall().decode())
break
if __name__ == "__main__":
auto_guess()02 mouse-trail
通过题目得知是绘画的坐标系，写一个py脚本
import matplotlib.pyplot as plt
# 读取坐标文件
def read_coordinates(file_path):
coordinates = []
with open(file_path, 'r') as file:
for line in file:
try:
x_str, y_str = line.strip().split(',')
x, y = int(x_str), int(y_str)
coordinates.append((x, y))
except ValueError:
# 忽略无效行
continue
return coordinates
# 主程序
file_path = 'mouse_movements.txt' # 请确保该文件存在于当前目录
coordinates = read_coordinates(file_path)
# 拆分 x 和 y
x_vals, y_vals = zip(*coordinates)
# 绘制图形
plt.figure(figsize=(12, 8))
plt.scatter(x_vals, y_vals, s=10, color='blue')
plt.title("Scatter Plot of Coordinates")
plt.xlabel("X Coordinate")
plt.ylabel("Y Coordinate")
plt.grid(True)
plt.tight_layout()
plt.show()这个时候会得到一个图片，我们可以发现是镜像的图片，通过反转可以发现flag。
03 make-groups
这道题是让我们计算一个大组合数乘机，作为结果输出flag。
# calc_fast.py
MOD = 998244353
def precompute_factorials(n, mod):
factorial = [1] * (n + 1)
inv_fact = [1] * (n + 1)
for i in range(1, n + 1):
factorial[i] = factorial[i - 1] * i % mod
# 费马小定理求逆元
inv_fact[n] = pow(factorial[n], mod - 2, mod)
for i in range(n - 1, -1, -1):
inv_fact[i] = inv_fact[i + 1] * (i + 1) % mod
return factorial, inv_fact
def choose(n, r, fact, inv_fact):
if r < 0 or r > n:
return 0
return fact[n] * inv_fact[r] % MOD * inv_fact[n - r] % MOD
def main():
with open("chall.txt") as f:
lines = f.read().splitlines()
n = int(lines[0])
a = list(map(int, lines[1].split()))
fact, inv_fact = precompute_factorials(n, MOD)
ans = 1
for x in a:
ans = ans * choose(n, x, fact, inv_fact) % MOD
print(f"tjctf{{{ans}}}")
if __name__ == "__main__":
main()04 golf-hardester
一个正则高尔夫挑战，要用尽可能短的正则表达式，匹配一组给定的字符串，同时排除另一组字符串。
第一关
打开kali直接nc连接，发现一列全是a开头，一列全是其他字母开头。
我们要匹配所有左侧的单词，排除右侧单词，所以直接^a就可以进入下一关（使用最小长度匹配特征，完美符合“正则高尔夫”哲学：最短路径完成目标。）
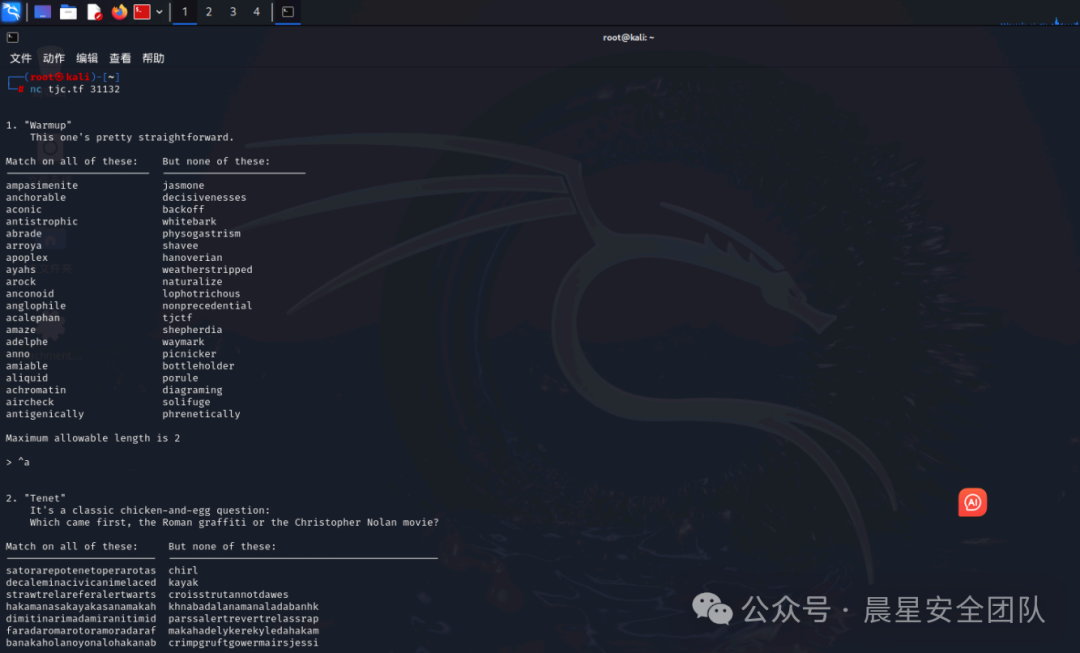
第二关
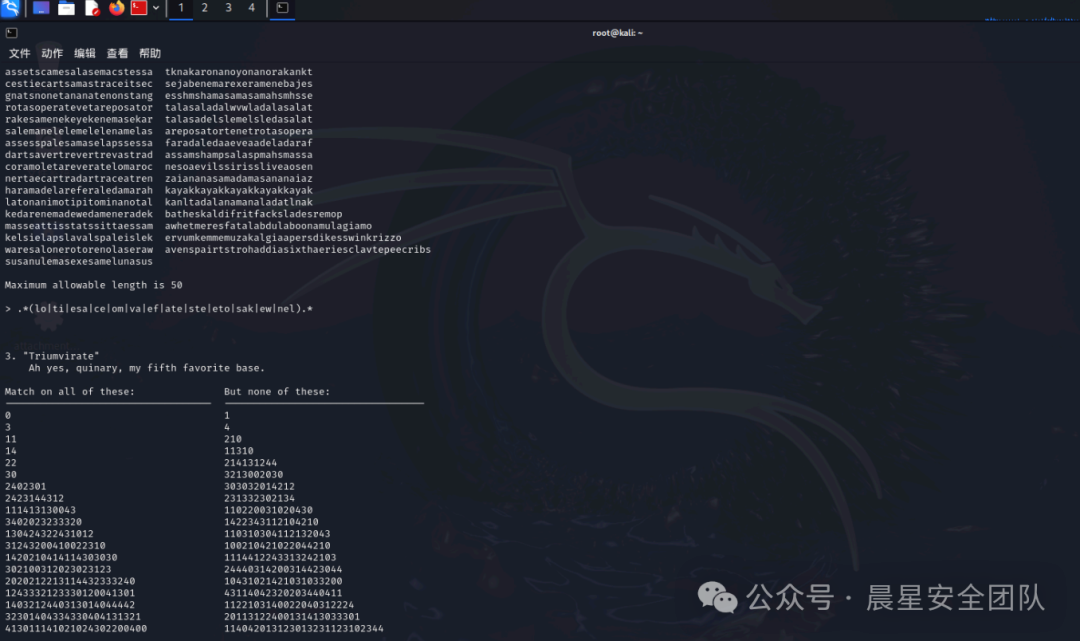
要求是匹配所有回文串，排除非回文串。细看字符串中都对应的匹配了某些片段特征，而非对映里面都不包含以下这些字符串。
.(lo|ti|esa|ce|om|va|ef|ate|ste|eto|sak|ew|nel).*
第三关
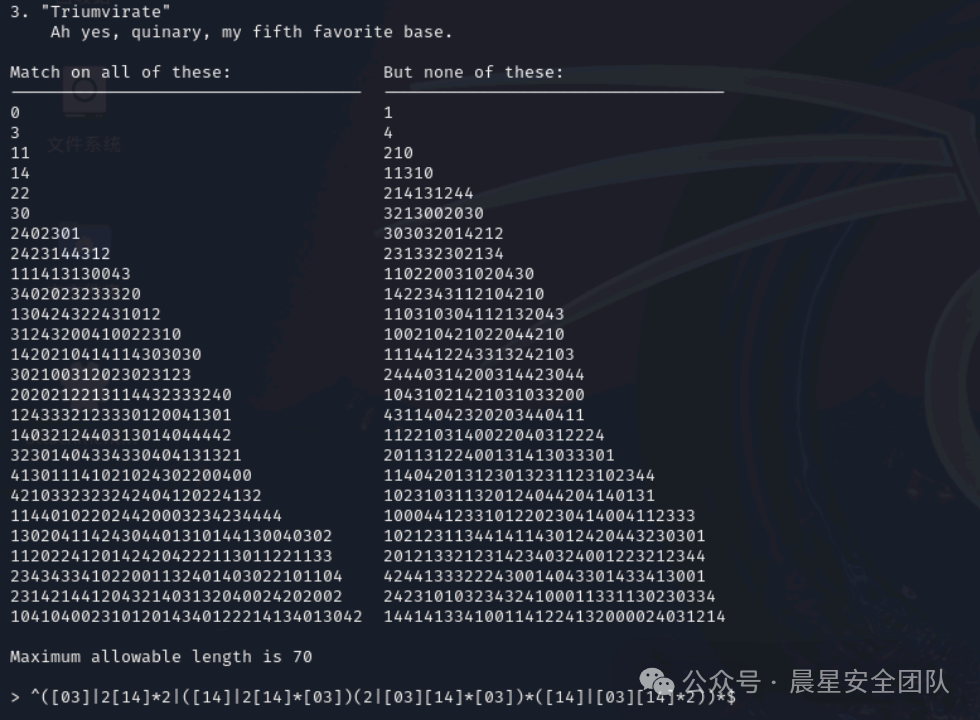
"Ah yes, quinary, my fifth favorite base."
提示我们这是base-5（五进制）数字匹配题。
应匹配的全都是由字符、符∈0–4
能匹配的合法样本：
不合法的样本则无法匹配：
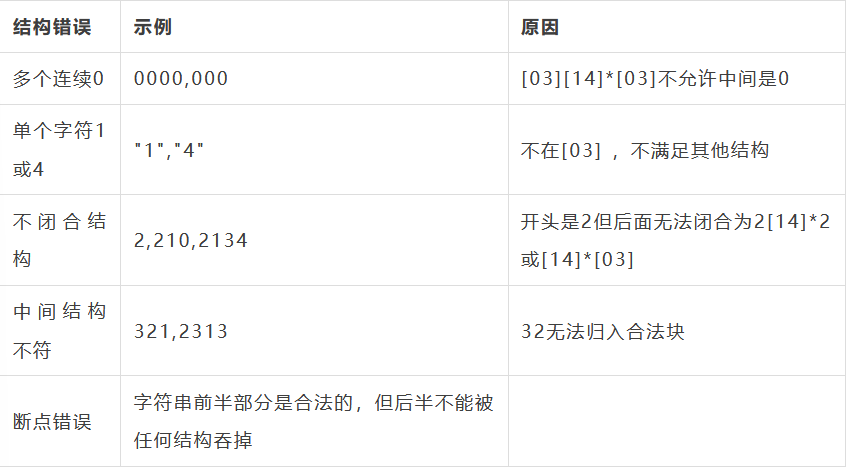
我们举个合法样本的例子：
302100312023023123
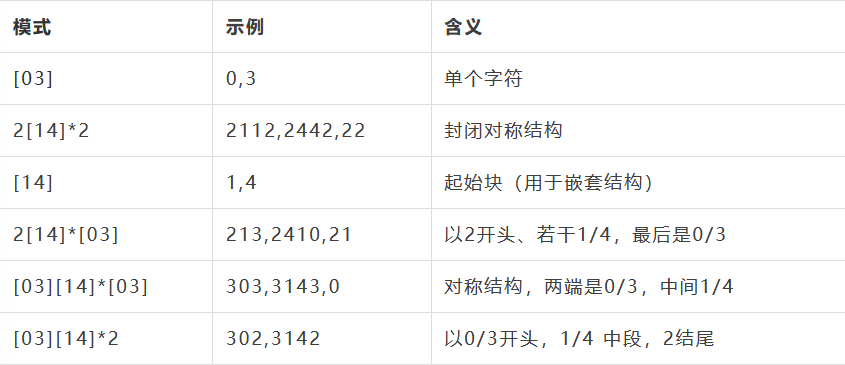
分段结构如下：
- 3 → [03]
- 0 → [03]
- 21 → 2[14]*[03]
- 002 → 0[14]*0 、再接 2
- 302 → [03][14]*2
- 3 → [03]
每一部分都能在正则结构中找到匹配块 。
再举一个不合法样本的例子：
1441413341001141224132000024031214
问题点如下：
- 0000 → 不在任何 [03][14][03] ，也不是 2[14]2 ，非法
- 32 → 不在 2[14][03] 也不在 [03][14]2 ，非法
- 剩余部分中段结构断裂、无法闭合
总结：你的字符串能否完全由这些结构块拼接起来？能就合法，不能就不匹配
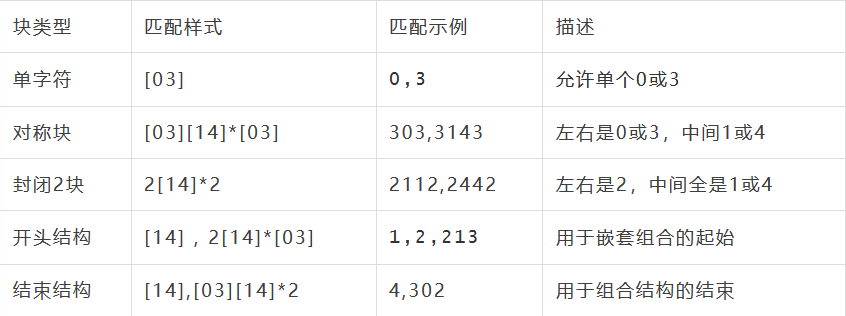
这个时候就可以写出一个正则匹配的字符串
^([03]|2[14]*2|([14]|2[14]*[03])(2|[03][14]*[03])*([14]|[03][14]*2))*$
解释就可以为
^(
[03] # 单字符 0 或 3（基础单元）
|
2[14]*2 # 一个 2 开头、1/4 任意次、2 结尾
|
(
[14] | 2[14]*[03] # 起始块：1或4，或2开头配0/3
)
(
2 | [03][14]*[03] # 中间块：2 或者 0/3包裹1/4
)*
(
[14] | [03][14]*2 # 结束块：1/4，或0/3包裹结尾2
)
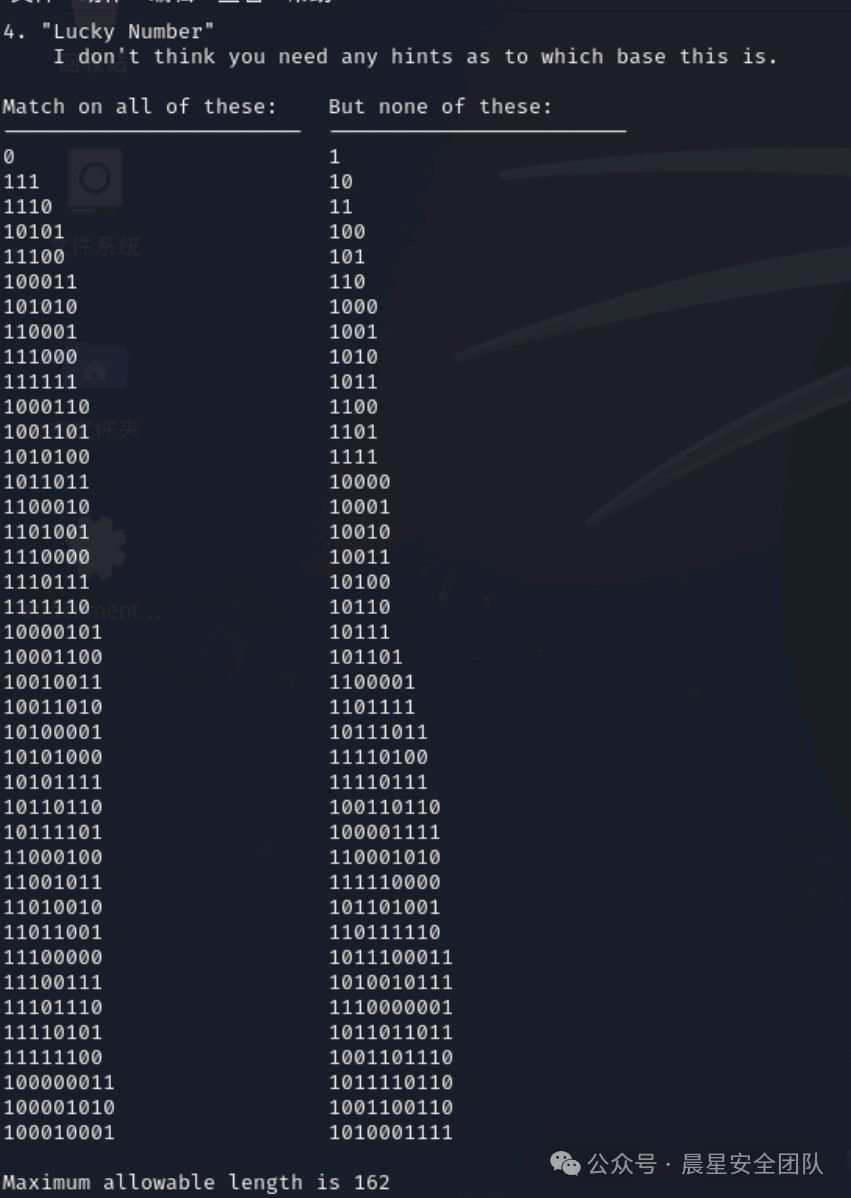
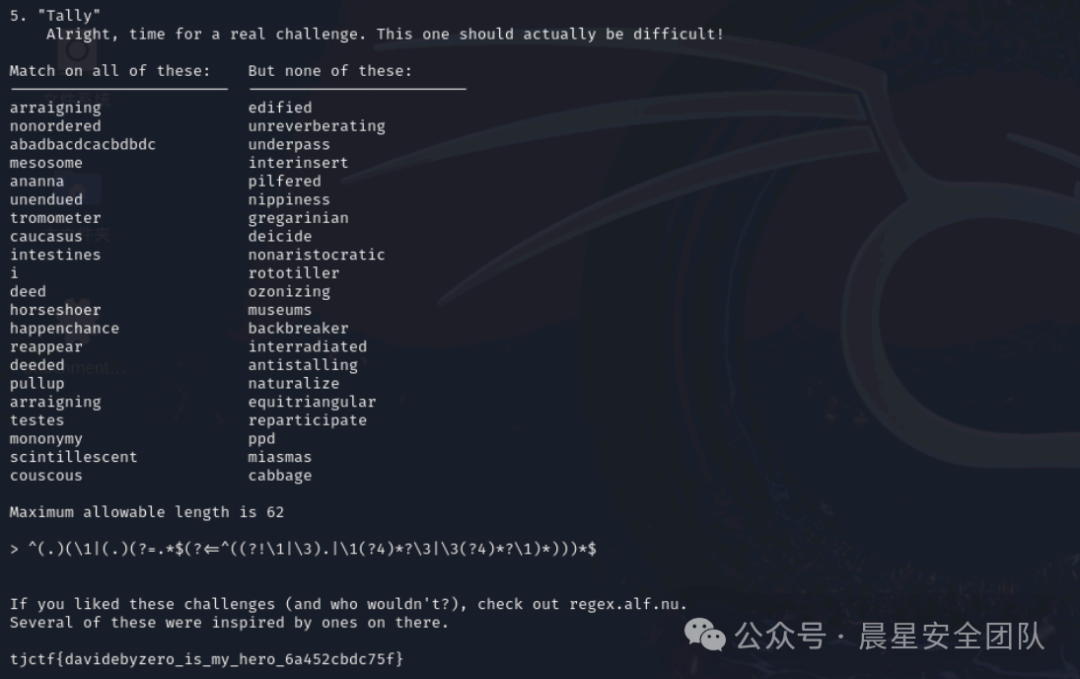
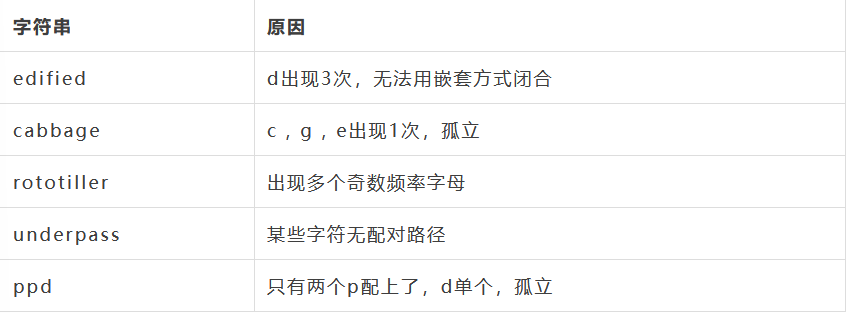
)*$第四关
标题暗示我们是一个二进制匹配的内容
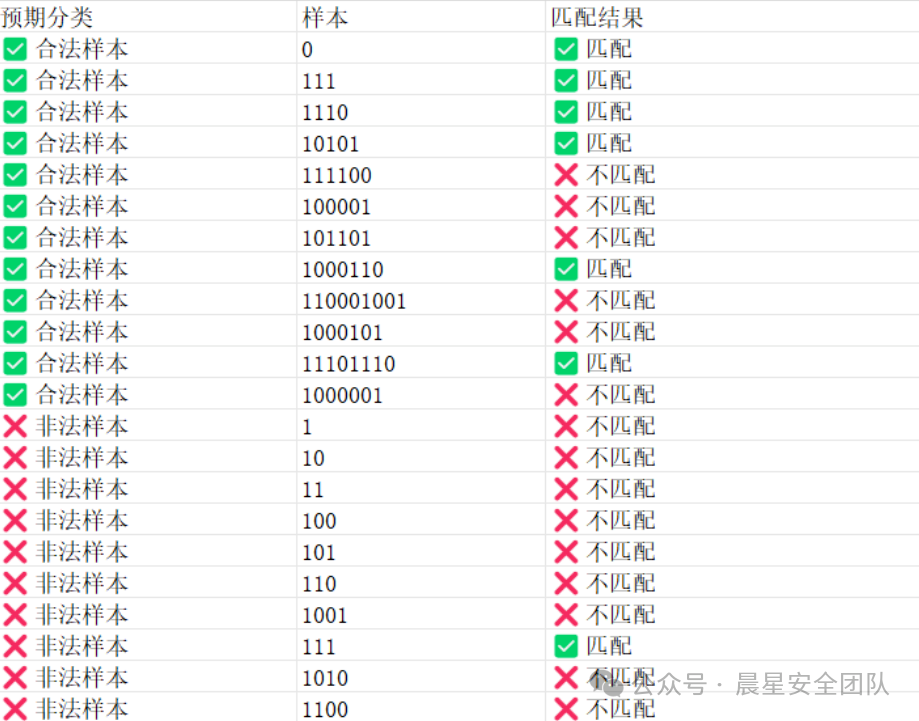
0单独存在的时候是合法行为，而1单独存在的时候则是不合法，只有3个1和6个1都单独的时候是合法，其他都是不合法行为。
通过将合法数据和不合法数据对比跑脚本得出：
所以按照合法样本可以写一个正则匹配为
^(0|(((0|111)|10(0(1|00))*0011)|(110(1)*0|10(0(1|00))*(1|0010(1)*0))(((00(1)*0|1010(1)*0)|1(1|00)(0(1|00))*(1|0010(1)*0)))*((01|1011)|1(1|00)(0(1|00))*0011)))*$
第五关
通过合法例子能发现
再去查看不合法的例子
判断的条件则是
通过最后可以写出一个正则为
^(.)(\1|(.)(?=.*$(?<=^((?!\1|\3).|\1(?4)*?\3|\3(?4)*?\1)*)))*$
分析可以得出
^
(.) # 捕获第一个字符到 \1
(\1 # 若第二字符是同一个 \1 → 匹配
|
(
. # 否则捕获一个新字符 \3
(?=
.*$
(?=^(
(?!\1|\3). # 不等于 \1 或 \3 的
|
\1(?\4)*?\3 # \1 之后 \3 之后再回 \1
|
\3(?\4)*?\1 # 或 \3 之后 \1 之后再回 \3
)*)
)
)
)*
$
最终的flag是：tjctf{davidebyzero_is_my_hero_6a452cbdc75f}作者：晨星安全团队--Zion_Cat